I recently got interested in database indexes and want to know how exactly they work. Going through tutorials is one thing but building something from scratch gives you deeper knowledge, so that’s what I did.

I also wanted to roughly benchmark each iteration so I can figure out where exactly does the code spent most of its time.

How does the data looks?

I kept things pretty simple. I created a CSV file with autoincremented id and username fields. The program would simply read from it and create an in-memory index. The index can be queried by id and it will return the whole row (id & username).

// sample file
1,abs
2,add
3,ccc

There are two metrics I was most interested in - Index Building Time and Query Time. I calculated them in every iteration.

Iteration #1: Simple BST

Ok, so the first attempt was just to create a simple BST, read CSV file, build index and query the index. The node struct was

struct Node {
    int id;
    int lineNum;
    Node *left;
    Node *right;
};

As you can see, I was just storing line numbers instead of whole rows to reduce memory footprint. Also, as the data is pretty structured and I can pinpoint the exact byte I have to start reading for a given id. I guess the same logic is being used by popular DBs (still have to verify though).

In this attempt, I got following results (numbers are in microseconds):

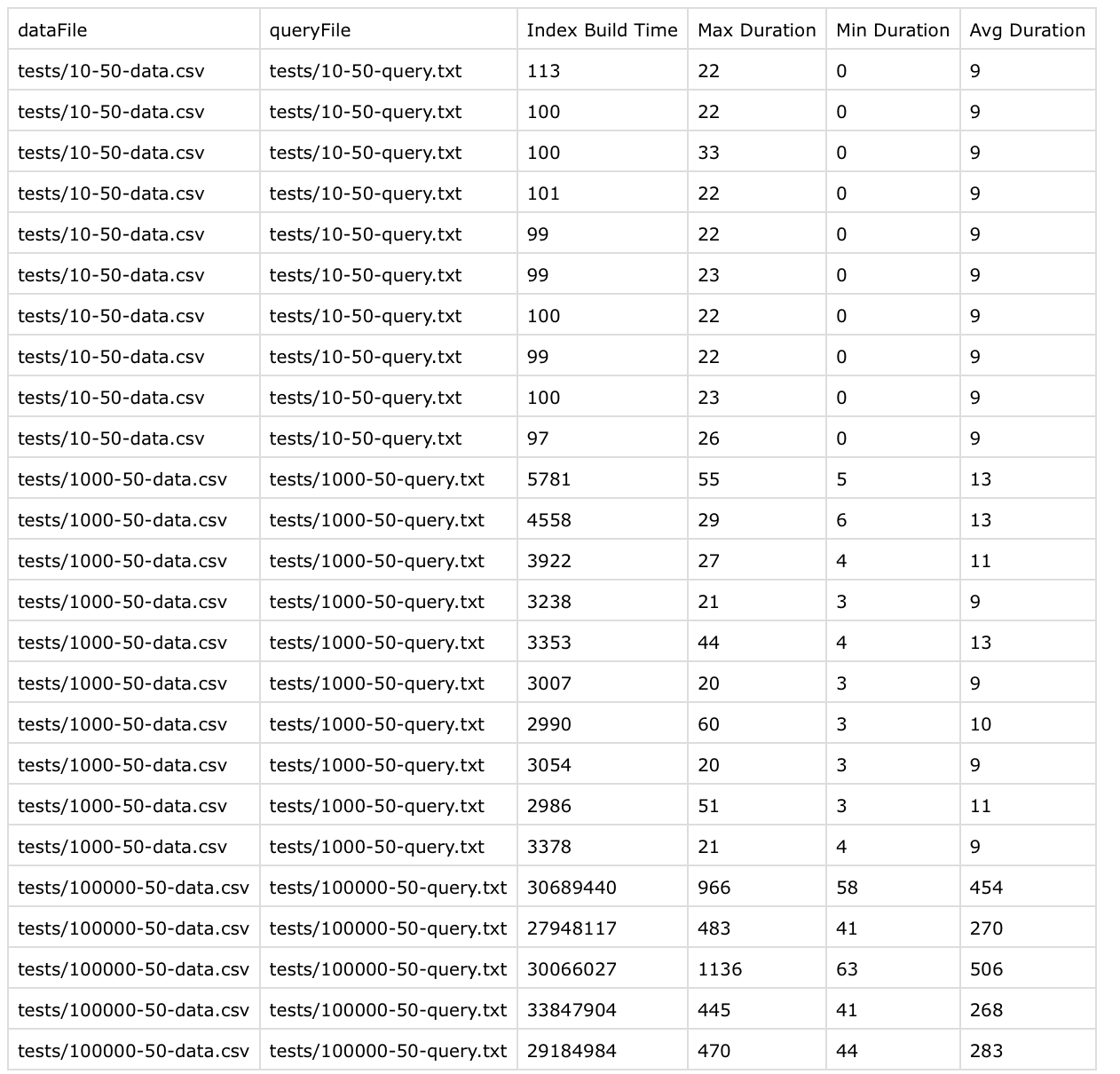
side note: tests/10-50-data.csv means 10 rows with 50 queries, similary tests/100000-50-data.csv means 100000 rows with 50 queries

Okay, so index creation was getting pretty worse (~30 secs) as the number of rows increases. This was expected as the index wasn’t balanced and was just a linear list. Every insertion was taking O(n) time.

The obvious optimization here was to somehow balance the tree during insertion. It will reduce both insertion and query time.

Iteration #2: Self Balancing BST (partially wrong AVL implementation)

There are two popular ways to balance BST - AVL and Red-Black. I went ahead with AVL. The basic principle of AVL is:

• Insert the node normally (which you will probably do recursively)
• While recursing-back, calculate the height of the left subtree & the right subtree. If the difference b/w then is more than 1 then this tree is not balanced.
• Balance the tree (there are 4 cases) and you are done

Here are the result of this iteration:

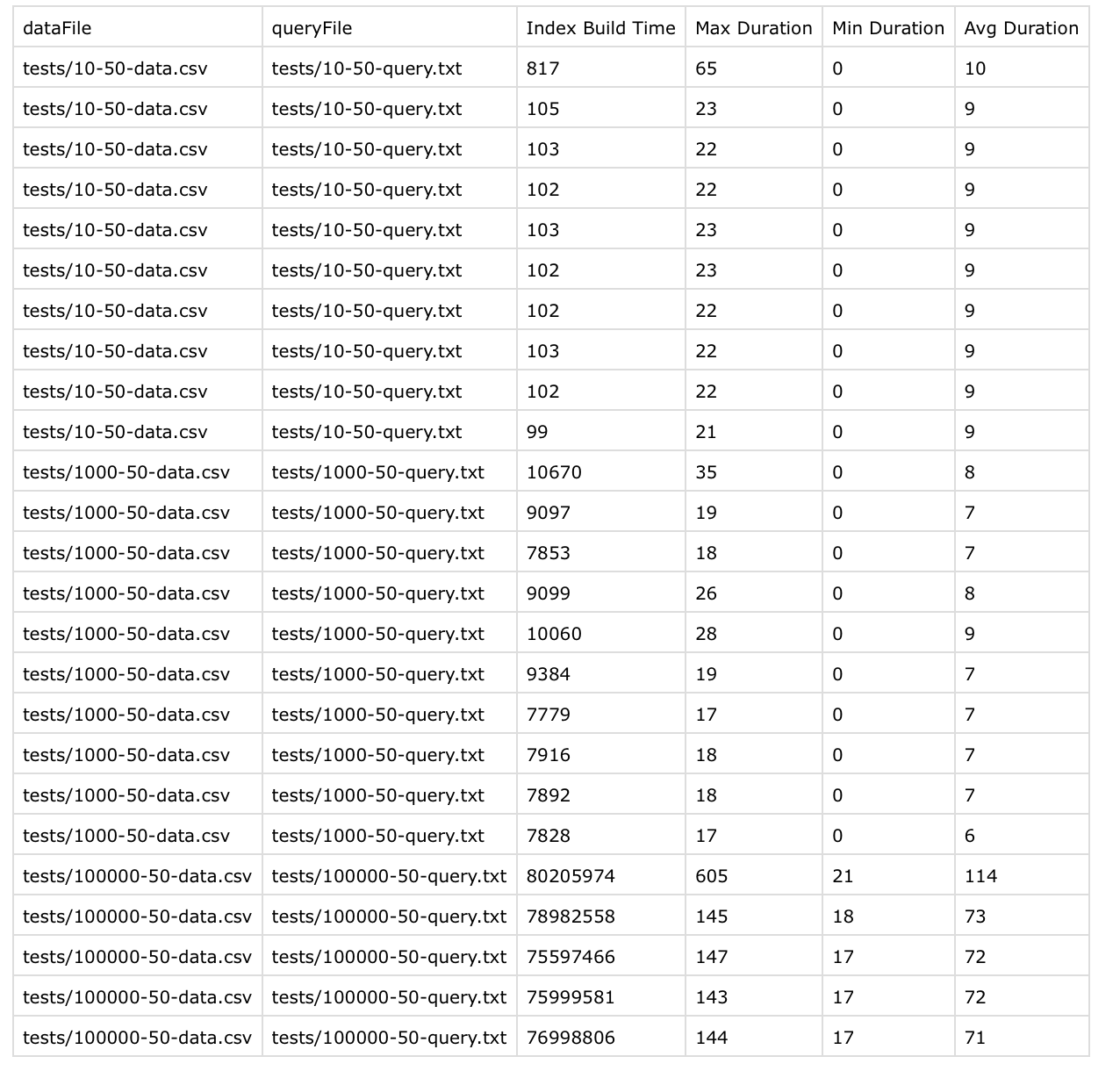
Insights from this iterations:

• Insertion time almost doubled which is expected because the program is calculating tree height on every node [optimization here is to store tree heights in the node itself]
• Query time was reduced by almost 4.5 times which signifies that the tree is now more balanced.
• I tried submitted same code to a problem in a leetcode which required to build us a BST using AVL but it was failing on few cases.

Iteration #3: Self Balancing BST (correct AVL implementation with balancing on just 1 node)

I rewrote the AVL insertNode code again as the last code was failing on leetcode and might not be truly balanced. I also kept a global bool to do balanced at max once after each insertion.

Both of these optimizations resulted in:

• insertion time of ~0.13 seconds for tests/100000-50-data
• query time of < 10 microseconds in all test cases
• able to process tests/1000000-50-data and run it within seconds. The total index build time was ~1.5 seconds which is really great. Query time is also < 10 microseconds which is amazing given the tree size of 1 million nodes.

Here are the results

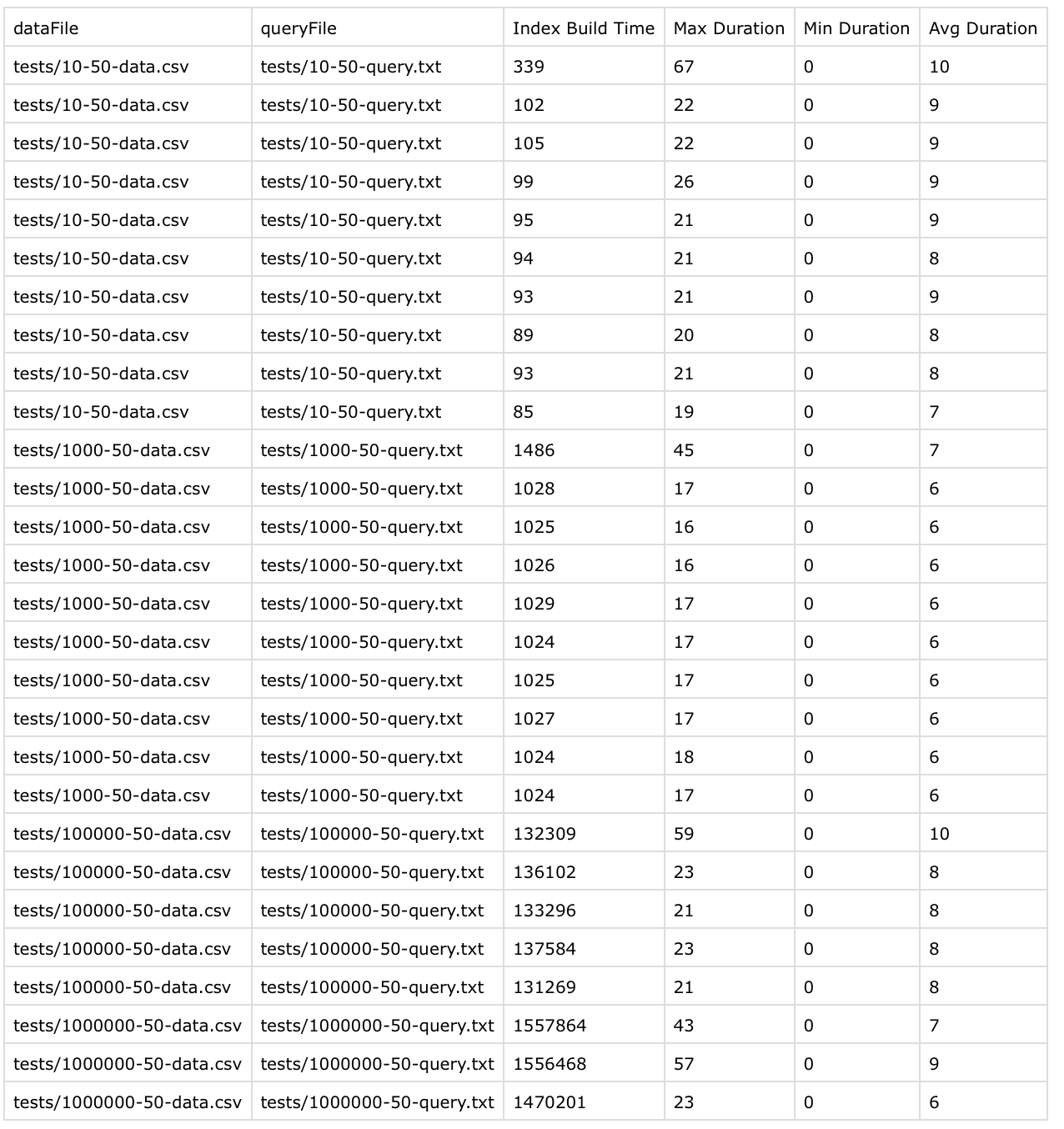
Results are pretty amazing here but there is still one routine I can optimize. The program would work efficiently if the insertion results in a non-balanced tree but what if the insertion didn’t make the tree non-balanced?

In that case, the program was calculating tree heights on every node until the root. This is the piece I wanted to optimize next.

Iteration #4: Self balancing BST (AVL + storing left and right tree heights on node itself)

In this iteration, I started storing height of left subtree & right subtree on the node as well. The logic to update heights while doing balancing were pretty complex but doable nonetheless.

Here are the results

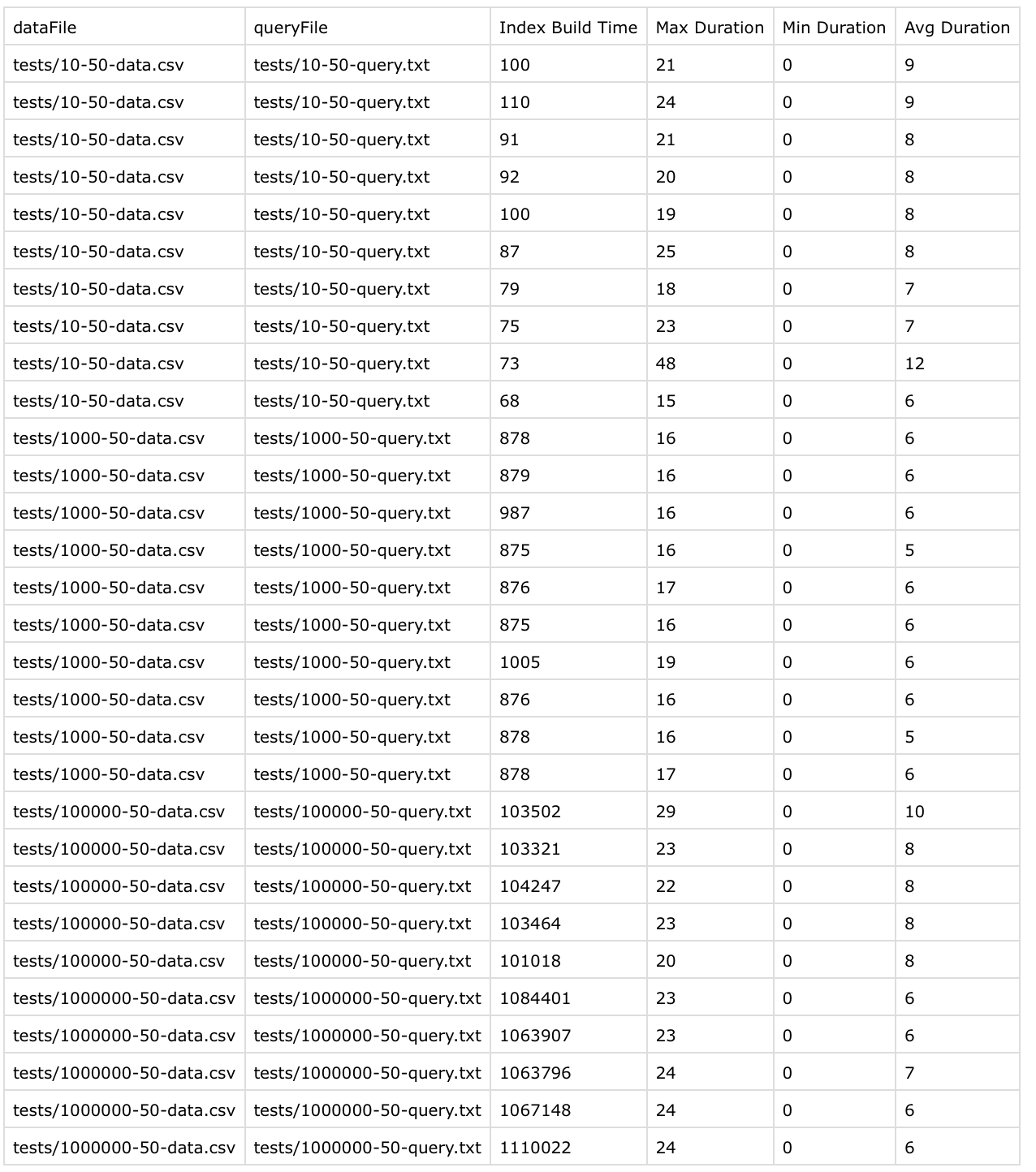
I was able to reduce build time from ~1.5 seconds to ~1 second while keeping query time well below 10 microseconds.

What’s next?

• Benchmark performance on ranged queries
• Implement index using B-Tree & compare performance
• Implement text based index. Support like kind of queries as well
• Implement composite index